一、CT图像重建：

CT图像重建是最早的三维成像技术，在医学、工业和科学研究中有着重要应用。实验室课题组主要研究（不完全数据的）CT图像正则化重建模型和算法。由Beer定律，二维CT图像重建的数学问题是反演（平行束或扇形束）Radon变换（1）

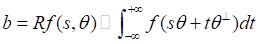                                                                     (1)

其中 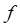   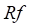 ,     分别为被重建图像和采样数据。当数据不完全时，CT图像重建时严重病态问题，我们提出了基于二阶全变差（2）和L1正则化（3）的CT图像重建模型。

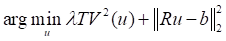                                                                                                 (2)

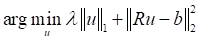                                                                      (3)

其中 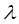    是正则化参数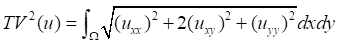，     。二阶全变差模型的重建图像如图（1）所示

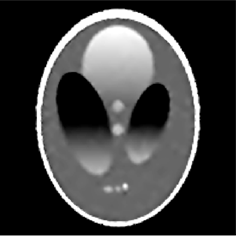
原图                                二阶全变差方法                              一阶全变差方法

图一

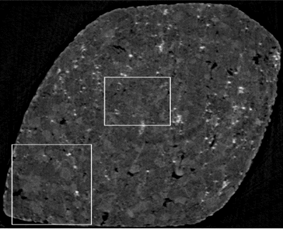
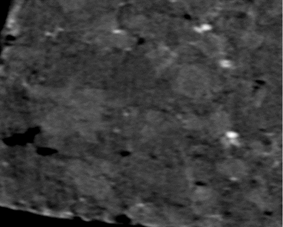
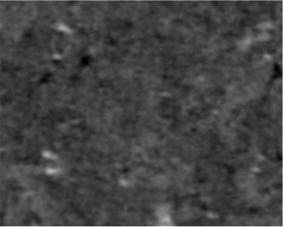
L1正则化方法重建图像                             CT设备重建图像

图2： 实测数据重建图像

二、并行核磁共振成像（parallel Magnetic Resonance Imaging, pMRI）

和 CT技术相比，MRI更适合软组织成像，而且能实现组织器官的功能成像，是现代医学影像学的重要技术。从数学上看，MRI设备采集的数据为成像目标的Fourier变换，通过Fourier逆变换即可得到成像目标。但是传统的MRI设备扫描所有频率的数据所需的时间较长，不合适对与时间有关的目标成像（如胸腔的成像）。并行MRI使用多个线圈分别采集部分频率数据，达到加速数据扫描的目的。此时的MR图像重建问题是不适定问题，需要借助正则化方法实现高质量MR图像重建。基于噪声在频域（K空间）的特点，我们提出了

                                                   

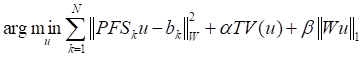
其中 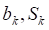    分别为第 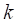    个线圈的采样数据和感知矩阵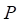，     为下采样矩阵（重建图像见图3）

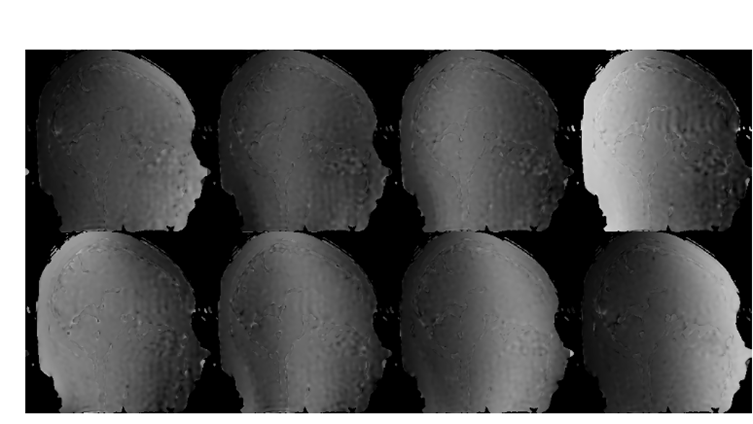
8个线圈的感知矩阵

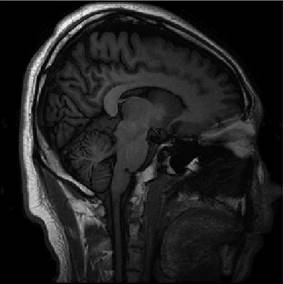
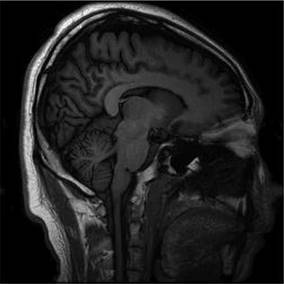
    L2拟合项                                                  自适应加权L2拟合项